معادله رشد و زوال ( -ODE+SDE Exponential growth)
معادله به فرم \(dx_t=b.x_t.dt\) را معادله رشد و زوال (ساده) گویند . بسته به اینکه \(b >o \) رشد و افزایش و در صورتی که همین ضریب منفی باشد با کاهش یا زوال روبرو هستیم .
حل این معادله در حالت قطعی (deterministic) بسیار ساده است . به روال زیر نگاه کنید .
\(\begin{cases}\frac{dx}{dt}=b.x \\x(0)=x_0\end{cases}\)
:حال داریم
\(dx=b.xdt\\ \int_{0}^{t}\frac{dx}{x}=\int_{0}^{t}bds\)
\(\ln x(t)-\ln x(0)=bt \\\ln \frac{x(t)}{x(0)}=bt \\ \frac{x(t)}{x(0)}=e^{bt}\\x(t)=x_0e^{bt}\)
در این حالت نکته مبهم یا پیچیده ای نداریم ،با توجه به مقدار اولیه همه چیز به سرعت معلوم می شود
اما فرض کنیم که در مدل رشد و زوال مورد نظر نویز وجود داشته باشد . یعنی مثلا یکسال رشد با نرخ 2 درصد و سال دیگر با نرخ 2.3 و دیگری با نرخ 2.1 وباز نرخ بعدی 1.98 و…باشد .می خواهیم مدلی را بیان کنیم که حاوی چنین اطلاعاتی باشد . پس با شکل زیر روبرو هستیم
\(\begin{cases}\frac{dx}{dt}=b.x +”noise”\\x(0)=x_0\end{cases}\)
:اگر نویز مورد نظر دارای توزیع نرمال باشد(گاوسی) در این صورت می توان معادله را به شکل زیر نمایش داد
\(\begin{cases}dx_t=b.x_t.dt +\sigma .x_t.dW_t\\x(0)=x_0\end{cases}\)
که در اینجا سیگما ضریب بزرگی نویز می باشد . به چنین معادله ای معادله رشد و زوال تصادفی (Stochastic) :گویند . و برای حل آن به این صورت عمل می کنیم، تابعی کمکی را بصورت زیر تعریف می کنیم
\(g(t,x)=\ln x,\space \frac{dx_t}{x_t}=b.dt+\sigma.dW_t\)
:طبق فرمول ایتو داریم
\(dg=\frac{\partial g}{\partial t}dt+\frac{\partial g}{\partial x}dx+\frac{1}{2}\frac{\partial^2 g}{\partial x^2}(dx)^2\)
: اگر مشتقات جزیی را محاسبه کنیم خواهیم داشت
\(\frac{\partial g}{\partial t}=0\\\frac{\partial g}{\partial x}=\frac{1}{x}\\\frac{1}{2}\frac{\partial^2 g}{\partial t^2}=\frac{1}{2}(\frac{-1}{x^2})\)
:با قرار دادن در فرمول دیفرانسیل ایتو خواهیم داشت
\(\large dg=0dt+\frac{1}{x}dx+\frac{1}{2}\frac{-1}{x^2}(dx)^2\)
: با قرار دادن رابطه \(dx_t=b.x_t.dt +\sigma .x_t.dW_t\)در دیفرانسیل ایتو داریم
\(\large dg=0dt+\frac{1}{x}(b.x.dt +\sigma .x.dW_t)+\frac{1}{2}\frac{-1}{x^2}(b.x.dt +\sigma .x.dW_t)^2\)
:حال با فاکتور گیری و ساده سازی داریم
\(\large dg=0dt+\frac{1}{x}(b.x.dt +\sigma .x.dW_t)+\frac{-1}{2x^2}(b.x.dt +\sigma .x.dW_t)^2\\
\large dg=\frac{1}{x}x(bdt +\sigma .dW_t)+\frac{-1}{2x^2}x^2(bdt +\sigma .dW_t)^2\)
:ادامه می دهیم
\(\large dg=(bdt +\sigma .dW_t)+\frac{-1}{2}(b^2(dt)^2 +\sigma^2 .(dW_t)^2+2b.\sigma .dt.dW_t)\)
:می دانیم که
\(\large (dt)^2 \to 0 \\(dW_t)^2 \to dt\\dt.dW_t \to 0 \)
:پس با قرار دادن در رابطه فوق خواهیم داشت
\(\Large dg=(bdt +\sigma .dW_t)+\frac{-1}{2}(0+\sigma^2 .dt+0)\\dg=(b-\frac{1}{2}\sigma^2).dt+\sigma .dW_t\)
:طرف چپ عبارت دیفرانسیل کامل است . پس اگر از طرفین انتگرال بگیریم ، خواهیم داشت
\(\large \int_{0}^{t} dg=\int_{0}^{t}(b-\frac{1}{2}\sigma^2).ds+\int_{0}^{t}\sigma .dW_s\\
g(t)-g(0)=\int_{0}^{t}(b-\frac{1}{2}\sigma^2).ds+\int_{0}^{t}\sigma .dW_s\\
\ln(x(t))-\ln(x_0)=\int_{0}^{t}(b-\frac{1}{2}\sigma^2).ds+\int_{0}^{t}\sigma .dW_s\\\ln\frac{x(t)}{x_0}=\int_{0}^{t}(b-\frac{1}{2}\sigma^2).ds+\int_{0}^{t}\sigma .dW_s\\\frac{x(t)}{x_0}=e^{\int_{0}^{t}(b-\frac{1}{2}\sigma^2).ds+\int_{0}^{t}\sigma .dW_s}\\x(t)=x_0.e^{\int_{0}^{t}(b-\frac{1}{2}\sigma^2).ds+\int_{0}^{t}\sigma .dW_s}\)
اگر در مساله مقدار \(b, \sigma\)ثابت باشند . در این صورت عبارت به فرم ساده تر زیر در می آید .
\(\Large x(t)=x_0.e^{(b-\frac{1}{2}\sigma^2)t+\sigma .\int_{0}^{t}dW_s}\\x(t)=x_0.e^{(b-\frac{1}{2}\sigma^2)t+\sigma W_t}\)
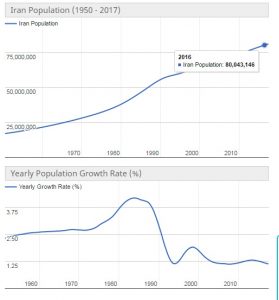
به نمودار جمعیت و تغییرات رشد جمعیت ایران نگاه کنید . در حقیقت این فرایند نمایی ساده نیست
و این جدول جمعیت ایران در خلال سالیان و نرخ تغییرات ، نرخ زاد و ولد و رتبه ایران در جهان را به لحاظ جمعیت نشان می دهد
| Year | Population | Yearly % Change |
Yearly Change |
Fertility Rate | World Population | Iran Global Rank |
| سال | جمعیت | درصد تغییرات سالانه | تغییرات سالانه | نرخ زاد و ولد | جمعیت دنیا | رتبه ایران در جهان |
| 2017 | 80,945,718 | 1.13 % | 902,572 | 1.72 | 7,515,284,153 | 17 |
| 2016 | 80,043,146 | 1.18 % | 933,874 | 1.72 | 7,432,663,275 | 17 |
| 2015 | 79,109,272 | 1.27 % | 971,180 | 1.75 | 7,349,472,099 | 17 |
| 2010 | 74,253,373 | 1.15 % | 826,252 | 1.79 | 6,929,725,043 | 17 |
| 2005 | 70,122,115 | 1.27 % | 854,411 | 1.97 | 6,519,635,850 | 17 |
| 2000 | 65,850,062 | 1.77 % | 1,106,286 | 2.63 | 6,126,622,121 | 17 |
| 1995 | 60,318,632 | 1.44 % | 829,887 | 3.95 | 5,735,123,084 | 16 |
| 1990 | 56,169,196 | 3.5 % | 1,775,681 | 5.62 | 5,309,667,699 | 20 |
| 1985 | 47,290,793 | 4.11 % | 1,724,514 | 6.53 | 4,852,540,569 | 22 |
| 1980 | 38,668,222 | 3.39 % | 1,187,533 | 6.28 | 4,439,632,465 | 22 |
| 1975 | 32,730,555 | 2.8 % | 843,309 | 6.24 | 4,061,399,228 | 25 |
| 1970 | 28,514,011 | 2.7 % | 711,779 | 6.68 | 3,682,487,691 | 25 |
| 1965 | 24,955,116 | 2.64 % | 609,642 | 6.91 | 3,322,495,121 | 26 |
| 1960 | 21,906,905 | 2.57 % | 522,581 | 6.91 | 3,018,343,828 | 26 |
| 1955 | 19,293,998 | 2.42 % | 434,947 | 6.91 | 2,758,314,525 |
کپی برداری از مطالب با نقل قول آزاد است . ارادتمند خسروتاش